
Be specific! (b) Compute E-1 and ET (recall that Eis computed in MATLAB with the command E'), and observe that they are also permutation matrices. How are the two matrices related? Describe the effect on A of right multiplication by the permutation matrix E. Be specific! Compute the product AE and compare the answer with the matrix A. A.row perm A.row A.col perm A. How are the two matrices related? Describe the effect on A of left multiplication by the permutation matrix E. If you have a sparse matrix stored in COO format, the following might be helpful. Generate a 5 x 5 matrix A with integer entries using the command A = floor(10*rand(5)) (a) Compute the product EA and compare the answer with the matrix A.

Simply create a hash set for the given row. The time complexity for this approach will be O (mn log n). If any row is completely equal to the given row, that means the current row is a permutation of the given row. For example, we can construct O 0 1 0 07 0 0 0 1 0 E = 0 0 0 0 1 (2) 1 0 0 0 0 % permutation vector that defines % the new order of the rows E = eye (length(p)) % define E as the identity matrix E = E(p,:) % permute the rows of E according to the % permutation vector p The second command creates the 5 x 5 identity matrix, and the third command uses the vector p to permute its rows, so row P(1)= 3 becomes row 1, row p(2)=4 becomes row 2, row p(3)=5 becomes row 3 and so on (compare these row permutations with the vector p defined above).ĮXERCISE 3 If you haven't already done so, enter the commands in the example above to generate the permutation matrix E defined in (2) (you can suppress this matrix). A simple solution is to one by one sort all rows and check all rows. One way to construct permutation matrices is to permute the rows (or columns) of the identity matrix. In this section we will look at properties of permutation matrices.
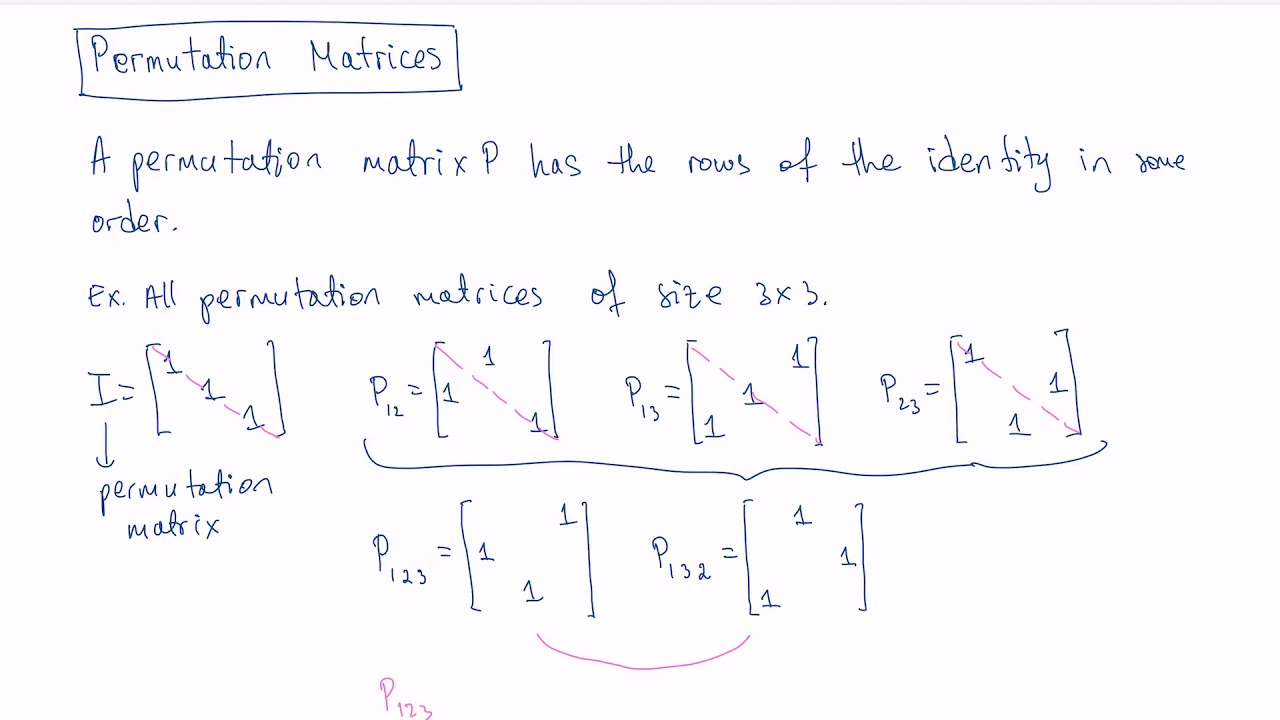
Matrix (vector) multiplication with permutation. Transcribed image text: Permutation matrices A permutation matrix is a square matrix that has exactly one 1 in every row and column and O's elsewhere. The pMatrix class is the class of permutation matrices, stored as 1-based integer permutation vectors.


 0 kommentar(er)
0 kommentar(er)
